תוֹכֶן

• צעדים
• טיפים

מתמטיקאים ומתכנתים גרפיים לעיתים קרובות צריכים למצוא את הזווית בין שני וקטורים. למרבה המזל, הנוסחה המשמשת לחישוב זווית זו אינה דורשת יותר ממוצר סקלרי פשוט. למרות שקל יותר להבין את ההנמקה העומדת מאחורי נוסחה זו בעת שימוש בווקטורים דו מימדיים, אנו יכולים להתאים אותה בקלות לווקטורים עם כל מספר רכיבים.

צעדים

חלק 1 מתוך 2: חשב את הזווית בין שני וקטורים

1. 

   זהה את שני הווקטורים. רשמו את כל המידע הידוע על שני הווקטורים. לצורך לימוד זה נניח שאתה מכיר את הווקטורים רק מבחינת הקואורדינטות הממדיות שלהם (נקרא גם רכיבים). אם אתה כבר יודע מודול אוֹ תֶקֶן מבין הווקטורים האלה (כלומר אורכם), תוכלו לדלג על כמה מהשלבים שלהלן.
   • דוגמא: נשקול את הווקטורים הדו-ממדיים = (2,2) ו- = (0,3). ניתן לכתוב מחדש את שני הווקטורים הללו כ- 2אני + 2j e = 0אני + 3j = 3j.
   • למרות שהדוגמה שלנו משתמשת בשני ווקטורים דו מימדיים, אנו יכולים להחיל את ההוראות שלהלן על וקטורים עם מספר רכיבים כלשהו.

2. 

   
   
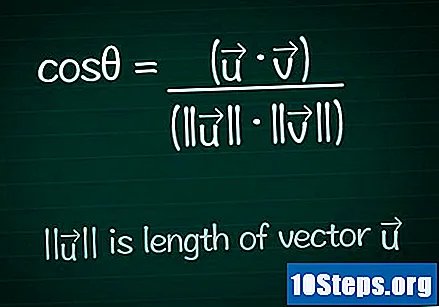
   כתוב את הנוסחה הקוסינוס. כדי למצוא את הערך של הזווית θ בין שני ווקטורים, עלינו תחשיב תחילה את הקוסינוס של אותה זווית. אתה יכול לחפש ולגלות את הנוסחה בפירוט או פשוט לכתוב אותה כפי שהיא למטה:
   • cosθ = (•) / (|||| ||||)
   • |||| מייצג את מודול (או אורך) של הווקטור ".
   • • מייצג את מוצר סקלרי (או מוצר פנימי) של שני הווקטורים.

3. 

   
   
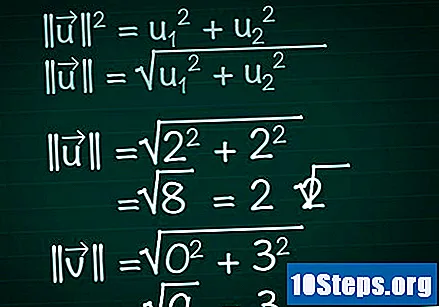
   חשב את המודולוס של כל וקטור. דמיין משולש ימין שנוצר על ידי הרכיב איקס של וקטור, המרכיב שלו y והווקטור עצמו. במשולש זה, הווקטור ממלא את תפקיד היפוזה; לפיכך, כדי למצוא את אורכה, אנו נשתמש במשפט פיתגורס. כתוצאה מכך, נוסחה זו ניתנת להחלה בקלות על וקטורים עם מספר רכיבים כלשהו.
   • || u || = u₁ + u₂. אם הווקטור כולל יותר משני רכיבים, פשוט המשך להוסיף + u₃ + u₄ +...
   • לכן, עבור וקטור דו ממדי, נצטרך לעשות זאת || u || = √ (u₁ + u₂).
   • בדוגמה שלנו, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   חשב את המוצר הסקלרי בין שני הווקטורים. עליך כבר לדעת את השיטה להכפלת וקטורים, הנקראת גם מוצר סקלרי. כדי לחשב את המוצר הסקלרי של שני ווקטורים מבחינת הרכיבים שלהם, אנו מכפילים את הרכיבים באותו כיוון זה עם זה ואז מוסיפים את התוצאות של אותם מוצרים.
   • אם אתה עובד עם תוכניות גרפיקה ממוחשבות, בקר תחילה בקטע "טיפים" לפני שתמשיך.
   • במונחים מתמטיים, • = u₁v₁ + u₂v₂, איפה u = (u₁, u₂). אם הווקטור שלך כולל יותר משני רכיבים, המשך להוסיף + u₃v₃ + u₄v₄...
   • בדוגמה שלנו, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. זה הערך של המוצר הסקלרי בין הווקטורים לבין.

5. 

   החלף תוצאות אלה בנוסחת הקוסינוס. זכור, cosθ = (•) / (|||| || ||). חישבנו כבר את המוצר הסקלרי ואת המודול של שני הווקטורים. כעת, נחליף את הערכים הללו בנוסחה ונחשב את הקוסינוס של הזווית.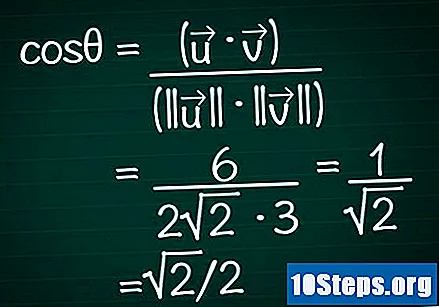
   • בדוגמה שלנו, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   מצא את הזווית על סמך הקוסינוס שלך.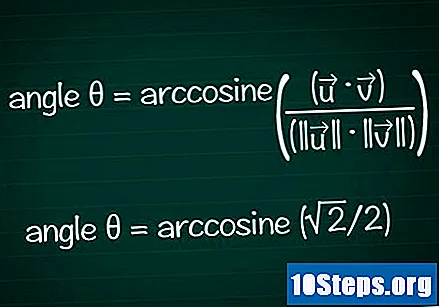
   השתמש בפונקציית הקשת או ה- cos של המחשבון שלך כדי לקבוע את הזווית θ מערך הקוסינוס שלך. במקרים מסוימים יתכן שתמצא את ערך הזווית על בסיס מעגל היחידה.
   • בדוגמה שלנו, cosθ = √2 / 2. הקלד "ארקוס (√2 / 2)" במחשבון שלך כדי למצוא את הזווית. אפשרות נוספת היא לחפש את הזווית θ של מעגל היחידה בה cosθ = √2 / 2: זה נכון θ = /₄ או 45 °.
   • כשאנחנו מחברים את כל המידע, תהיה לנו הנוסחה הסופית θ = ארקוזין ((•) / (|||| || ||))

חלק 2 מתוך 2: הגדרת הנוסחה לחישוב הזווית

1. 

   הבן את מטרת הנוסחה. הנוסחה בה השתמשנו לחישוב הזווית בין שני ווקטורים לא נגזרה מכללים שקיימים מראש; במקום זאת, הוא נוצר כהגדרה של המוצר הסקלרי בין שני ווקטורים והזווית ביניהם. עם זאת, החלטה זו אינה שרירותית. במבט מקרוב על הגיאומטריה הבסיסית, אנו יכולים לראות מדוע נוסחה זו מביאה להגדרות כה שימושיות ואינטואיטיביות.
   • הדוגמאות הבאות עושות שימוש בווקטורים דו מימדיים מכיוון שהם הסוג האינטואיטיבי ביותר איתו ניתן לעבוד. ווקטורים בעלי שלושה ממדים או יותר הם המאפיינים שלהם מוגדרים מהנוסחה הכללית (גם בצורה דומה מאוד).

2. 

   עיין בחוק הקוסינוס. בכל משולש יש לקחת בחשבון את הזווית θ שנוצרה על ידי הצדדים ה ו ב והצד ç מול הזווית ההיא. על פי החוק הקוסיני, c = a + b -2abחגורת המותן(θ). את ההדגמה של נוסחה זו ניתן להשיג בקלות מהידע בגיאומטריה בסיסית.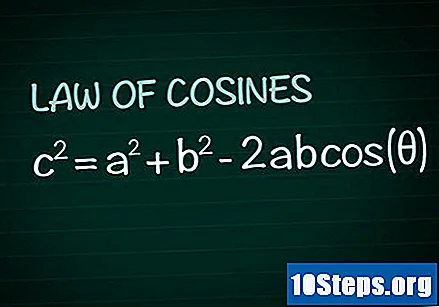

3. 

   חבר את שני הווקטורים ליצירת משולש. צייר זוג וקטורים ועם זווית θ ביניהם. ואז, צייר וקטור שלישי ביניהם ליצירת משולש. במילים אחרות, צייר את הווקטור כך + =, או פשוט = -.

4. 

   להחיל את החוק הקוסיני על משולש זה. החלף את אורך הצדדים של הצד שלנו משולש וקטורי (כלומר מודול הווקטור) בנוסחה לחוק הקוסינוס:
   • || (א - ב) || = || a || + || b || - 2 || א || || b ||חגורת המותן(θ)

5. 

   שכתב את הנוסחה באמצעות מוצרים סקלריים. זכור שמוצר הנקודה הוא הגדלה של וקטור אחד המוקרן על גבי אחר. המוצר הסקלרי של וקטור עצמו אינו מצריך הקרנה מכיוון שאין שינוי כיוון. משמעות הדבר היא ש- = || a ||. בהתבסס על מידע זה, בוא נכתוב את המשוואה של חוק הקוסינוס:
   • (-) • (-) = • + • - 2 || a || || b ||חגורת המותן(θ)

6. 

   פשט את הנוסחה. הרחב את המוצרים בצד שמאל של המשוואה ואז פשט אותם עד שתגיע לנוסחה שאנו מכירים לחישוב זוויות.
   • • - • - • + • = • + • - 2 || a || || b ||חגורת המותן(θ)
   • - • - • = -2 || a || || b ||חגורת המותן(θ)
   • -2 (•) = -2 || a || || b ||חגורת המותן(θ)
   • • = || א || || b ||חגורת המותן(θ)

טיפים

• לקבלת רזולוציה מהירה, החל את הנוסחה הבאה על כל זוג וקטורי דו ממדי: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• אם אתה עובד עם תוכניות גרפיקה ממוחשבות, סביר להניח שתצטרך לדעת רק את כיוון הווקטורים ולא את אורכם. בצע את הצעדים שלהלן כדי לפשט את המשוואות ולהאיץ את התוכנית שלך:
  • מנרמל כל וקטור, כלומר מצא את וקטור היחידה שיש לו כיוון זהה לזה של הווקטור המקורי. לשם כך, חלק את כל מרכיב הווקטור במודול הווקטור.
  • חשב את המוצר הסקלרי של הווקטורים המורמללים, לא את הווקטורים המקוריים.
  • מכיוון שהמודולוס (כלומר האורך) של הווקטורים המורמללים הוא יחיד, אנו יכולים להשאיר אותם מחוץ לנוסחה. המשוואה הסופית שלך לחישוב זוויות תהיה קשתות (•).
• על סמך הנוסחה של חוק הקוסינוס, אנו יכולים לגלות במהירות אם הזווית המדוברת היא חריפה או סתמית. התחל עם cosθ = (•) / (|||| ||||):
  • הצד השמאלי והימני של המשוואה חייב להיות בעל אותו סימן (חיובי או שלילי).
  • מכיוון שהאורכים הם תמיד חיוביים, cosθ תמיד יהיה זהה לזה של המוצר הסקלרי.
  • לכן, אם המוצר הסקלרי הוא חיובי, cos, יהיה חיובי. משמעות הדבר היא שהזווית נמצאת ברבע הראשון של מעגל היחידה, כלומר θ <π / 2 או 90 °. לכן הזווית חדה.
  • אם המוצר הסקלרי שלילי, cosθ שלילי. משמעות הדבר היא שהזווית נמצאת ברבע השני של מעגל היחידה, כלומר π / 2 <θ ≤ π או 90 ° <θ ≤ 180 °. לכן הזווית סתומה.